Designing a PWM Interface is easy, but using ST’s “HAL” layer requires a bit of testing. A friend of mine decided to write his own drivers because he believe ST’s drivers are over-complicated and too low level. I agree, but I prefer to make my own C++ Abstraction Layer on top of the drivers.
So how should a PWM Interface look like?
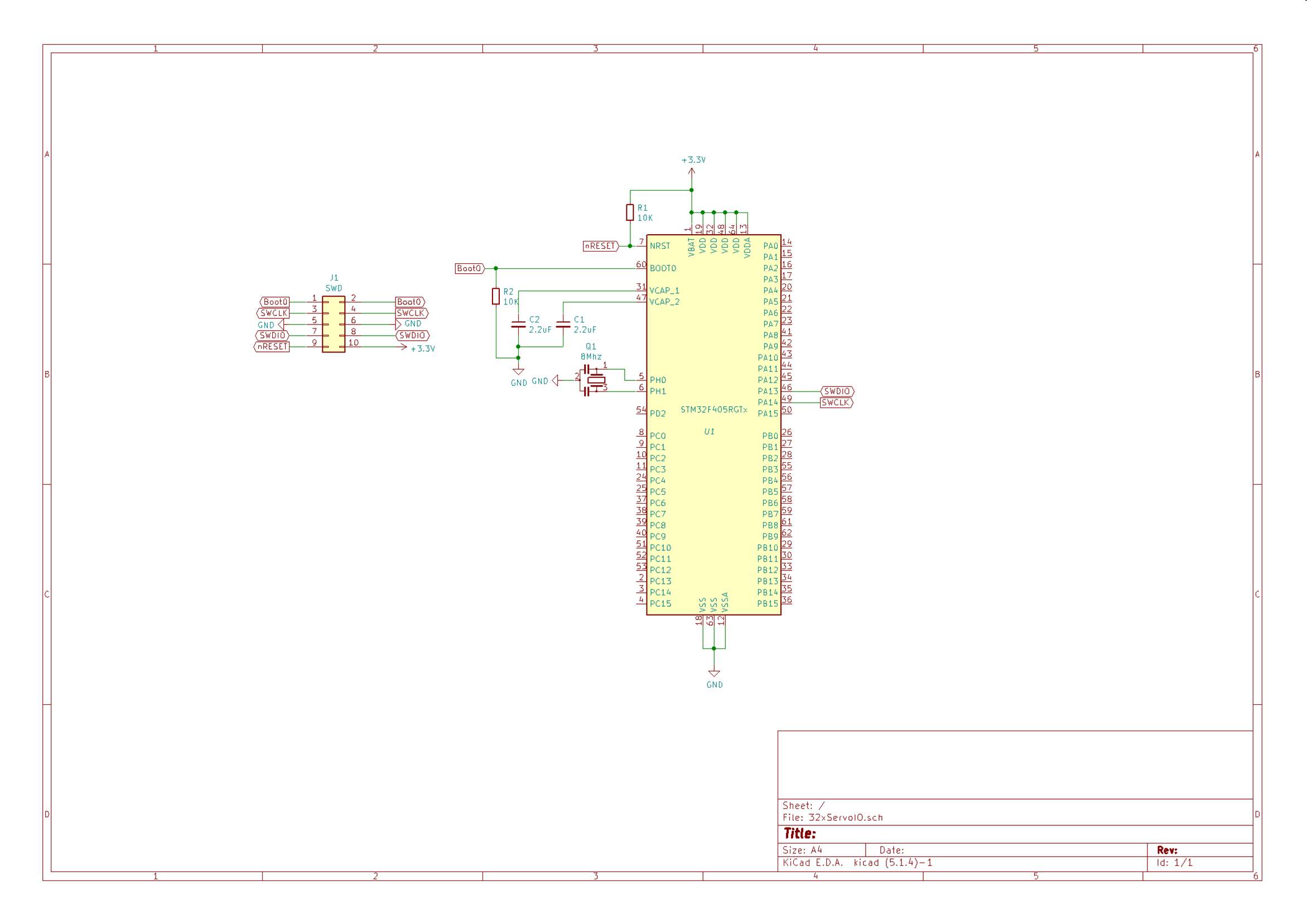
Using PWM we have one limitation. One timer control many PWM ports. The example below is from STM32F405RG
- TIM1 4 PWM signals
- TIM2 4 PWM signals
- TIM3 4 PWM signals
- TIM4 4 PWM signals
- TIM5 4 PWM signals
- TIM8 4 PWM signals
- TIM9 2 PWM signals
- TIM10 1 PWM signal
- TIM11 1 PWM signal
- TIM12 2 PWM signals
- TIM13 1 PWM signal
- TIM14 1 PWM signal
In total 32 PWM signals, but TIM1 as an example control 4 ports and those 4 signals must share the same frequency, but they have individual duty cycle. Channel 1–3 on Timer 1,2,3 and 8 are used in PWM12.
- – start/stop each channel.
- – Frequency configuration of timer in Hz. To make this simple I also add frequency on each channel knowing that if I configure channel 1,2 or 3 to different frequency I will change all 3 channels.
- – Duty Cycle in %
- – Manual On/Off. On is 100% Duty Cycle while Off is 0% Duty cycle.
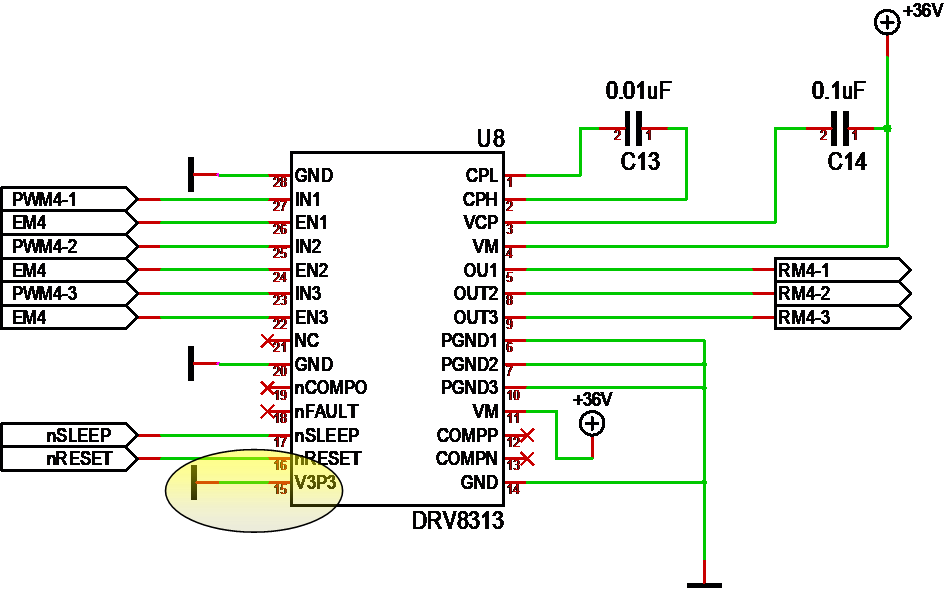
Wiring of PWM signals are the same as others. The same signal can be wired to different ports, so we wire each PWM signal to a Timer and Pin. This should be done in application initialization and is the only place where source code need to deal with physical layout.
This will work well for individual signals, but I also need to cover 3-Phase Motors, DC-Motors and Stepper motors in the Abstraction Layer as well as dual frequency signals.
A dual frequency means we pulse with a selected frequency and duty cycle and then use a secondary timer to create a lower pulse frequency based on that. This is an excellent way of providing PWM with an “amplitude”.
A 3-phase signal will use 3 or 6 PWM signals on a selected frequency – lets say 20Khz and then change duty cycle for each signal. If we use 64Khz we might want to change duty cycle only at 10Khz to avoid over-running the MCU as we need to do heavy math for each change.
DC is simpler as we use 2 signals and a selected frequency using duty cycle as speed (amplitude).
A stepper is even simpler as we use a trapezoidal algorithm to set position step by step. But, we can use the same trick with a higher frequency pulse to simulate amplitude and control torque.
This gives me the following AL classes:
- alPWM – single PWM signal
- alDCM – DC Motor composed of 2 PWM signals
- al3PM – 3-Phase motor composed of 3-6 PWM signals.
- alSTM – Stepper motor composed of 4 PWM signals.
In addition to the PWM side of things each class also need functionality to control it’s motor algorithm, but I leave that for a later entry.