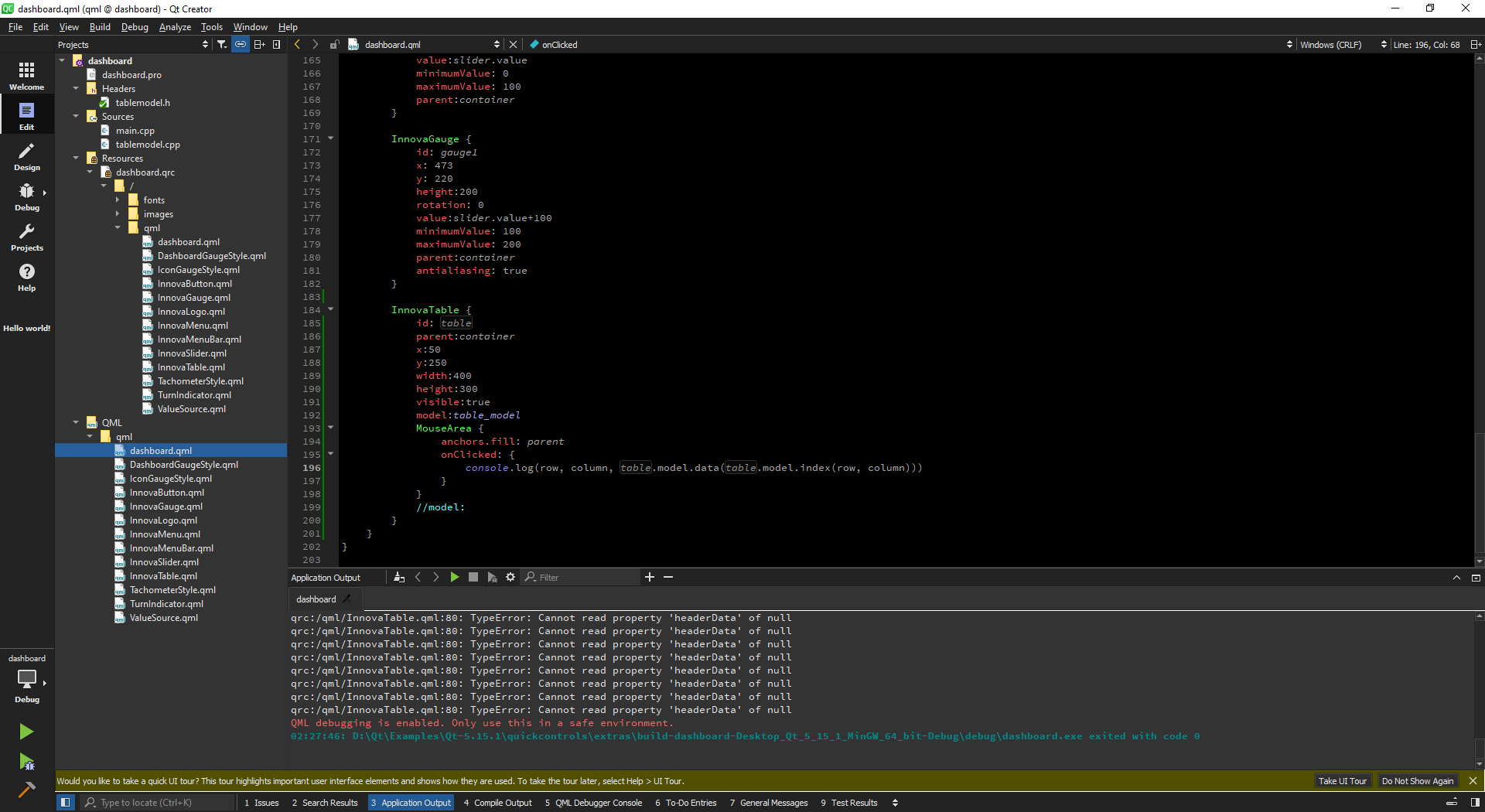
My previous entry talked about coding in QML. I am still on the learning path here, but I am slowly finding my way into QML. It is a steep learning curve, but once you start master the technology it also get easier and the graphical result is the best I have seen so far. It is complex with code in JavaScript, QML, Qt and C++ being combined. The alternative would be C# Core and WPF, but I have yet to learn that.
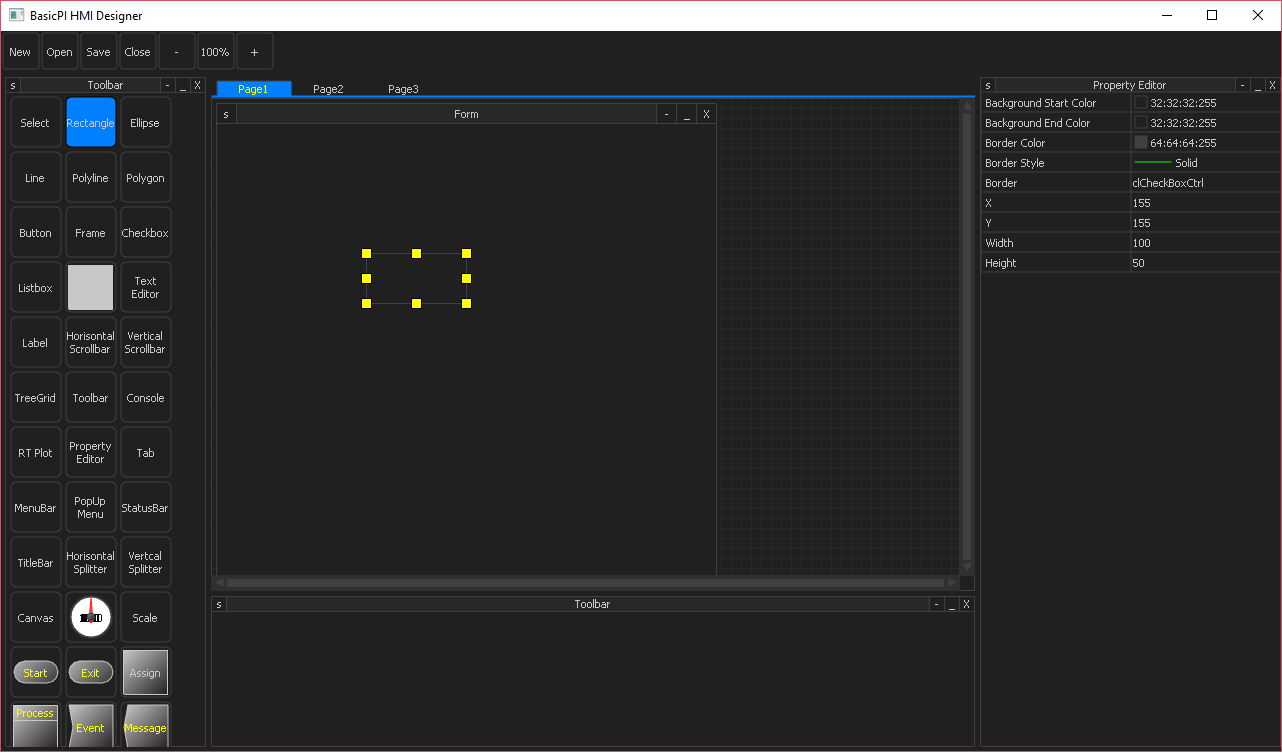
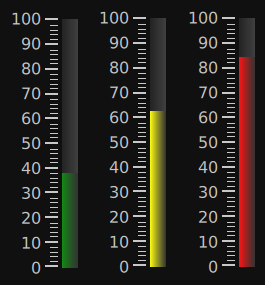
What you see above is the beginning of the HMI Designer. It does not look like much yet, but I am getting there. I am still planning a HMI Designer and associate HMI Browser to simplify advanced HMI design, but I will not stop there. I have yet to decide if I actually want to use Qt/QML for this as I am still on the learning side of things. As a C++ developer I can control my enthusiasm about Qt, but QML is a technology I so far have liked to work with.
The designers that are part of Qt have never really worked – I fail to understand why they can’t make a proper, visual HMI designer – it is not exactly rocket science. But, well – as you can see I am on my way of making my own. And my reasons have nothing to do with the non-working QT versions – I actually need this designer to be able to simplify HMI design to the level I want since the HMI designer is the first component of a complete system designer. This is about dramatically redusing the work-load needed to create well functioning, advanced systems.
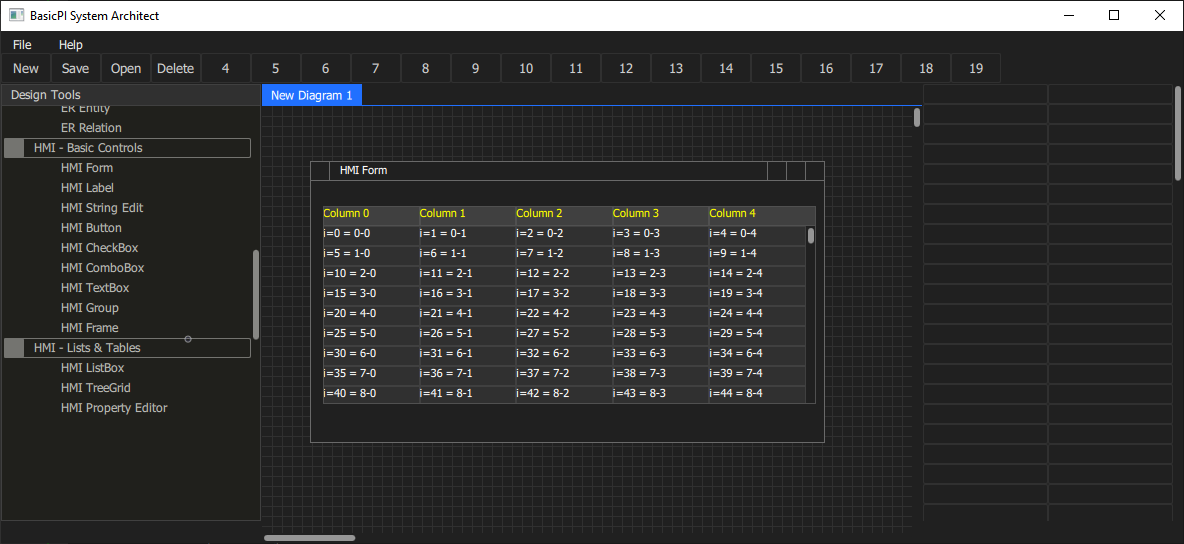
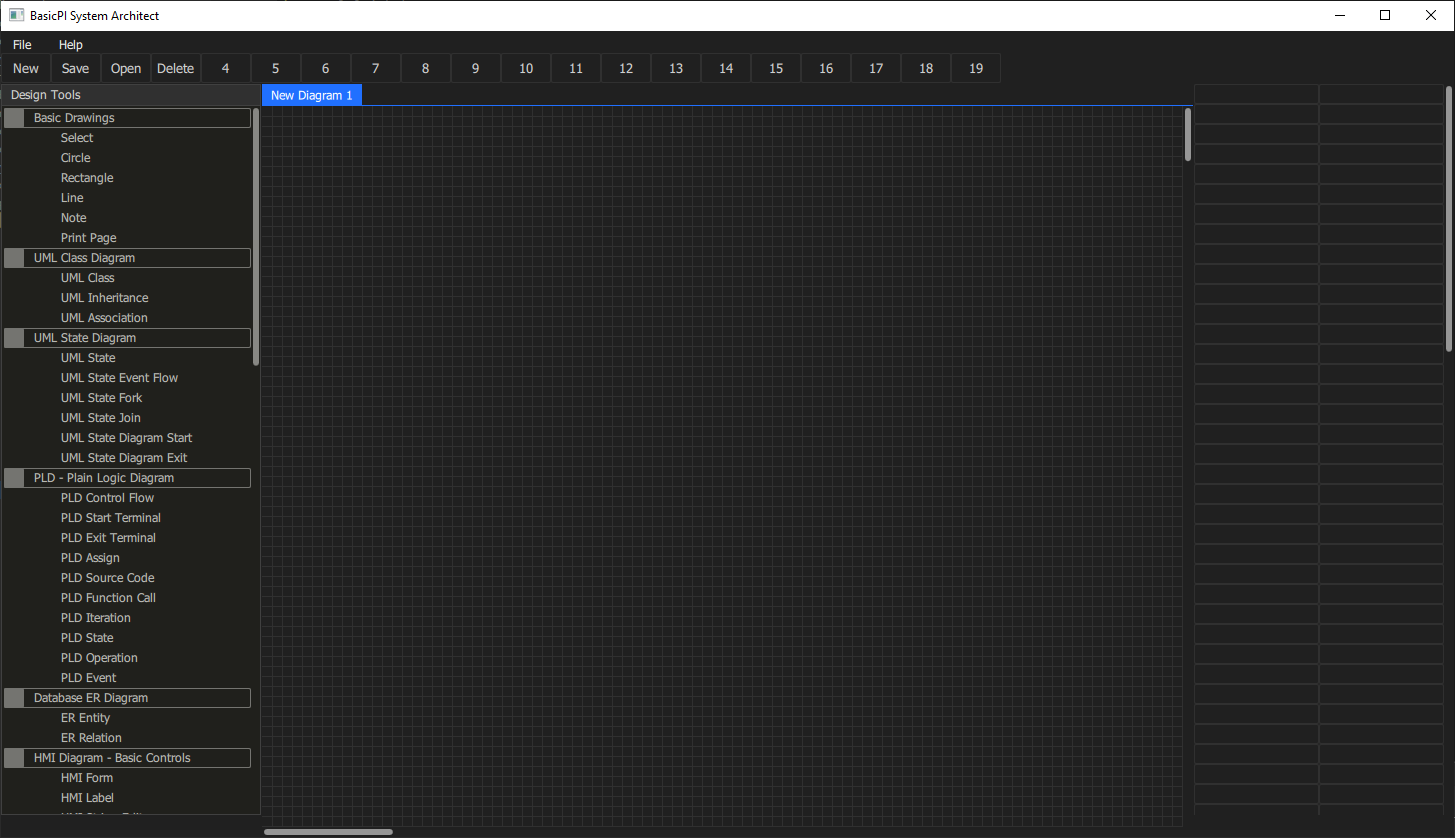
I am using a concept of universal diagrams – the diagrams can include multiple HMI Forms as well as other diagrams like UML mixed. At this point I will focus on HMI design and the code generators needed to generate the HMI part of the system. And don’t worry – you will be able to use this together with whatever GUI system you use be it Qt, QML, C# Forms, C#/WPF etc.
BSA will be using a Repository that basically is a JSON file and the code generators will be script based. Many like Phyton and JSON is well supported in Python, but I also plan a more specialized code generator script – something that I experienced with ca 25 years ago. I will return to that in a different blog entry.