In the Trapezoidal algorithm we drove the field using six steps which works, but it is very inaccurate. I would like more steps and to do that I need to use a Sinusoidal algorithm.
Sinusoidal means we create a sinus wave using PWM duty, in fact we create 3 sinus waves 120 degrees apart to rotate the field with more steps. To illustrate this I will build on the Trapezoidal algorithm and expand the number of steps it uses:
- A+ (100% duty), B- (100% duty) C (off)
- A+ (100% duty), (B- off), C- (100% duty)
This is out starting point. In the Trapezoidal example we applied the next step A+(100%/C-(100), but what we now will do is to move more gracefuly between B- to C- by adding 50% duty steps.
- A+ (100% duty), B- (100% duty) C (off)
- A+(100% duty), (B- 50% duty), C- (50% duty)
- A+(100% duty), (B- off), C- (100% duty)
By doing this we have basically modified a 6 step Trapezoidal to be a 12 step Sinusoidal and illustrated how we can use PWM duty to create a full sinusoidal algorithm.
 |
 |
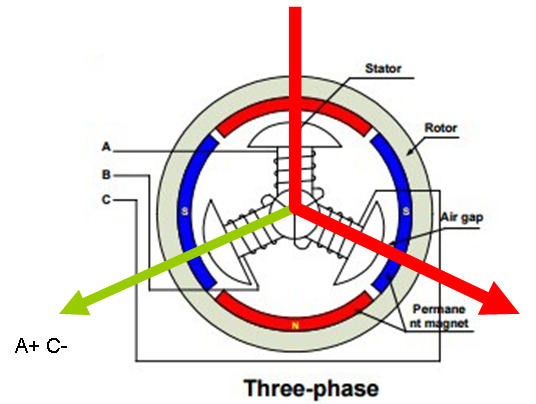The illustrations above illustrate the original Trapezoidal algorithm with the steps A+/B- and A+/C-. Vectors will in this case jump 45 degrees.
|
 |
|
The allistration above show the difference and what we achieve by introducing a new 50% duty step as we now have 22,5 degree jumps. We can now build on this and create a full 360 degree sinusoidal algorithm. Some Sinusoidal algorithms pre-calculate a 360 entry vector table with PWM out duty for A.B and C using index as the input vector. Assuming we use a 4 byte duty number (float) and 360 entries we end up with a 4320 byte lookup table. This is a decent tradeoff to avoid doing all the math real-time.
Just to remind everyone – the picture above is a common propeller motor and while it is still 3-phase it have something like 36 coils which will be A,B and C repeated over and over. This means that a 360 degree Sinusoidal and even a 6 step Trapezoidal might be far more accurate than you expect based on the theoretical 3-phase drawings. You need to know the number of coils to know your speed.